머신 러닝 알고리즘 : (Regression) - 랜덤포레스트
이번에는 랜덤포레스트(Random Forest) 알고리즘을 적용하여 동일한 데이터셋에 대해 예측을 진행해보자.
우선 랜덤포레스트란, 회귀 또는 분류 문제에 모두 사용할 수 있는 기계 학습 방법 중 하나이다.
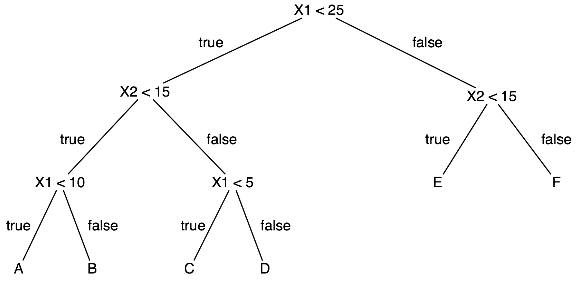
의사결정나무(Decision Tree)라고 하는 분류 알고리즘 여러개를 결합하는 앙상블 학습 방법이다.
이름에서 알 수 있는 것처럼, 의사결정나무가 모여 숲을 형성하는 것으로 이해하면 되겠다.
랜덤포레스트의 장점은 비교적 간단한 알고리즘과, 높은 예측력을 가지고 있으며 분류모델이다보니 스케일 변환이 필요없고 비선형데이터에 대해서도 잘 작동한다는 점이다. (선형/비선형 혼합 input 가능)
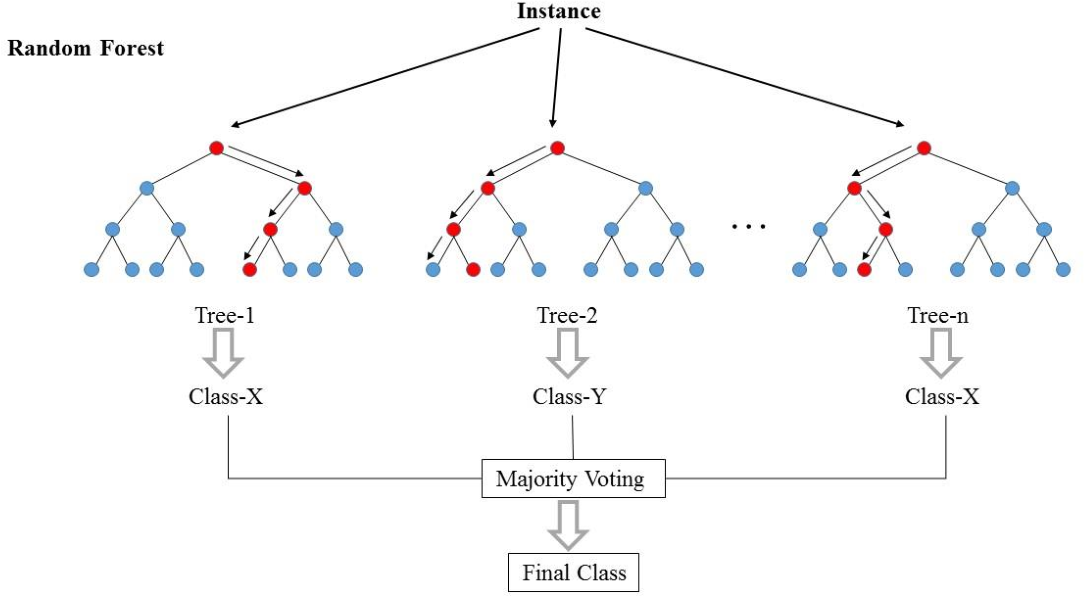
또한 여러개의 결정트리로부터 학습되어 결정한 모델이기 때문에 과적합될 가능성이 낮으며, 다중 입력값이 있을 때에는 각 변수마다 가중치(Importance) 를 계산해준다.
단점은 대량의 학습데이터가 존재할 때 메모리 사용량이 크고 느릴 수 있지만 강력한 예측 성능과 간단한 모델 사용법으로 여러 인공지능 모델링에 쓰이고 있다.
이제 boston 집값 에측 예제에 대해 적용한 결과를 확인해보자.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import warnings
warnings.filterwarnings('ignore')
# boston 집값 dataset 불러오기
train = pd.read_csv('train.csv')
# 수치형데이터 취합
train_data = train[['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE',
'DIS', 'RAD','TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']]
# 주어진 데이터에서 input 데이터와 output(추정하는 값) 으로 구분
X = np.array(train_data.iloc[:, 0:13])
y = np.array(train_data.iloc[:, 13])
# 주어진 데이터에서 train set 과 test set 으로 데이터를 구분
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 랜덤포레스트 회귀 모델 생성
# n_estimators : 트리의 개수, random_state : random seed 의 넘버(아무거나 상관없음)
rf = RandomForestRegressor(n_estimators=180, random_state=42)
rf.fit(X_train, y_train)
# fitting 한 모델을 통해 test data 의 target 변수를 예측
y_pred = rf.predict(X_test)
# r-squared 값 계산
r2 = r2_score(y_test, y_pred)
# 실측치와 예측치에 대한 scatter plot
plt.figure(figsize=(5,4))
plt.scatter(y_test, y_pred)
# 추세선 및 r-squared value 표시
z = np.polyfit(y_test, y_pred, 1)
p = np.poly1d(z)
plt.plot(y_test, p(y_test), "r--")
plt.text(20, 48, "R-squared = {:.3f}".format(r2))
# label 붙이기
plt.xlabel("Actual MEDV values")
plt.ylabel("Predicted MEDV values")
plt.title("Predicted MEDV values by RF")
plt.grid(True)
plt.show()
# 모델 성능 평가
mse = mean_squared_error(y_test, y_pred)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print("Mean Squared Error: {:.2f}".format(mse))
print("Mean Absolute Error: {:.2f}".format(mae))
print("R-squared Score: {:.2f}".format(r2))
# column 별 가중치 계산
feature_importances = pd.DataFrame({'feature': train_data.iloc[:, 0:13].columns,
'importance': rf.feature_importances_})
feature_importances = feature_importances.sort_values('importance', ascending=False)
print(feature_importances)train set 과 test set 의 비율은 7:3 으로 나누었고, 트리의 개수는 180개로 지정하였다.
시행결과 180개 이상의 estimator 에서는 동일한 결과를 보여주어 boston 데이터셋에서는 해당 값이 최적점으로 예상되는데, estimator 최적값을 찾는 방법에 대해서도 추후 학습해보기로 하고 일단 넘어가자.
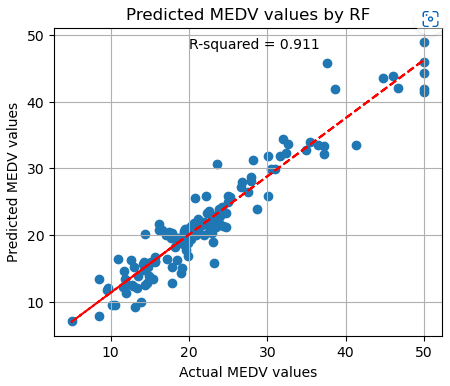

r-squared value 0.91 수준으로 예측 성능이 매우 우수한 결과를 나타내었다.
또한 오른쪽에 나타낸 것처럼 각 변수별 importance 를 구해주는 내장 함수가 있으니 참고하면 좋을 것 같다.
중요도가 낮은 변수는 제외하여 재학습을 하거나, 다른 분석 방식에 대한 성능 향상에 피드백으로도 유용할 것으로 예상된다.
다음 포스팅 에서는 신경망(Neural Network) 알고리즘의 기본인 Multi-Layer Perceptron 방식으로 확인해보자.
'Python' 카테고리의 다른 글
| [Python] Random Forest 최적화 방법 (0) | 2023.03.13 |
|---|---|
| 머신 러닝 알고리즘 : 선형 데이터 (Regression) - 뉴럴네트워크(MLP) (0) | 2023.03.09 |
| 머신 러닝 알고리즘 : 선형 데이터 (Regression) (0) | 2023.03.06 |
| class, class method 란? (0) | 2023.02.26 |
| random 패키지 (0) | 2023.02.26 |












